ASÍ CÚRVASE O ESPAZO

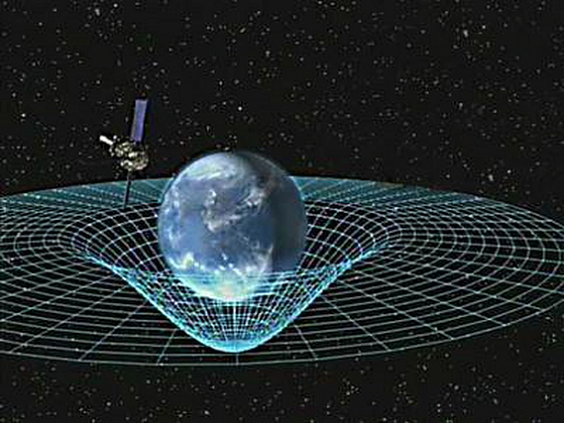
A sonda Gravity Probe-B mediu con máxima precisión o efecto do planeta Terra na curvatura do espazo-tempo.

Unha das ideas máis cativadoras da teoría da relatividad xeral de Albert Einstein é que a luz viaxa a velocidade constante, describindo traxectorias que minimizan a distancia entre puntos. Máis sorprendente aínda é a conclusión de que o espazo e o tempo deben curvarse para acomodar iste fenómeno. Que significa isto? Como son os espazos curvados? Que é a curvatura, e como se mide?

A curvatura fai referencia a unha calidade intrínseca que describe a forma do espazo tal e como sería percibida por unha persoa que vivise nel.

Dar unha definición precisa de que é a curvatura require de conceptos matemáticos avanzados, pero podemos describir a curvatura de maneira cualitativa nalgunhas situacións. Por exemplo, cando o espazo en cuestión é igual para todos os observadores (é dicir, é homoxéneo) e ten a mesma pinta en todas as direccións (isotrópico). Aínda que isto non é certo de maneira local para o noso universo (o Sistema Solar é moi diferente dunha rexión baleira), o principio cosmológico afirma que, en escalas espaciais suficientemente grandes, o Universo é isótropo e homoxéneo cumprindo coa conservación do momento angular e lineal, respectivamente.

Nestes espazos, a curvatura mídese polo defecto angular de triángulos. Si temos tres puntos no espazo, que conectamos polos camiños máis curtos entre eles (ollo, estes poden non ser liñas rectas, como ocorre no caso dunha esfera), obtense un triángulo con vértices neses puntos. Para obter o defecto angular calculamos a suma dos ángulos do triángulo e restamos 180º. O resultado (que pode ser positivo, negativo ou cero) é proporcional á área do triángulo, e o cociente do defecto angular pola área é precisamente a curvatura do espazo.

Se a curvatura é cero, atopámonos coa xeometría euclídea que estudamos na escola, onde todos os triángulos teñen ángulos que suman 180º. A este tipo de espazos chamámolos espazos planos. Cando a curvatura é positiva, os triángulos son máis gordos que os triángulos euclídeos, como os que un debuxa nunha esfera. Por esta razón, este tipo de espazos chámanse esféricos; por suposto, unha esfera é un exemplo deles. Finalmente, se a curvatura toma valores negativos , o triángulo é máis fino que un triángulo euclídeo, como o que debuxariamos na superficie dunha cadeira de montar, que recibe o nome de paraboloide hiperbólico. Por esta razón, este tipo de espazos chámanse espazos hiperbólicos. Dar exemplos de espazos hiperbólicos é máis complicado, aínda que podemos mencionar a pseudoesfera, que é a superficie que resulta de rotar a curva chamada tractriz ao longo dunha recta.

A maior parte da evidencia experimental (baseada na análise da radiación de fondo) suxire que o universo é plano a gran escala, cunha marxe de erro razoablemente pequeno. 

Visualizar a curvatura é máis sinxelo cando observamos superficies (obxectos de dúas dimensións) dentro do espazo tridimensional. Neste caso, a curvatura mide como e canto, a superficie retorcer no espazo. De maneira máis concreta, se a superficie ten curvatura positiva, cada un dos seus puntos parece unha cúpula; se a curvatura é cero, entón a superficie parece unha liña recta en polo menos unha dirección, como no caso dun plano ou un cilindro; finalmente, todo punto dunha superficie de curvatura negativa é un punto de cadeira: preto do punto, a superficie se curva “cara arriba” nunha dirección, e “cara abaixo” noutra, como ocorre preto dos bordos dunha folla de kale (follas rizadas de repolo).

En xeral, unha superficie pode ter puntos de curvatura positiva, negativa e nula, como ocorre coa superficie dun dónut. Si imaxinamos esta superficie apoiada no chan, os puntos do círculo interior teñen curvatura negativa; os do círculo exterior, curvatura positiva; e os dos círculos superior e inferior, curvatura cero.

Por suposto, ser capaz de observar un obxecto desde fóra ofrece un punto de vista inmellorable para describir a súa forma. Nesta situación, a curvatura fai referencia a unha calidade extrínseca da superficie, que describe a súa forma en función do espazo que a rodea. Non podemos dispor deste punto de vista no caso do noso universo, xa que non hai nada fóra del. Desta maneira, a curvatura convértese nunha calidade intrínseca e ofrece información sobre a forma do espazo tal e como sería percibida por unha persoa que vivise nel, sen ningún coñecemento dun espazo exterior, como ocorre co defecto angular.

O feito de que ambos os puntos de vista coinciden foi demostrado por un dos pais da xeometría moderna, o matemático alemán Carl Friedrich Gauss (1777-1885), quen quedou tan impresionado polo seu descubrimento que o chamou Theorema Egregium (teorema notable).

FONTE: Javier Aramayona/Jeffrey F. Broc/elpais.com/ciencia