SABÍAS QUE... ARITMÉTICA MODULAR

 

A aritmética modular foi estudada por primeira vez de forma sistemática por Carl Friedrich Gauss (1777-1855) no seu famoso Disquisitiones Arithmeticae de 1801. Algunhas veces chámaselle, suxerentemente, aritmética do reloxo, xa que os números «dan a volta» tras alcanzar certo valor chamado módulo.

Gauss definiu a congruencia da seguinte maneira: dous números enteiros a e b son congruentes módulo outro número n se o resto de dividir (sen decimais) a e b entre n é o mesmo. Isto é equivalente a que b - a sexa múltiplo de n. Por exemplo, 6 e 18 son congruentes módulo 12. É dicir, ao dividir 6 entre 12, obtemos como cociente 0 e como resto 6 e, doutra banda, ao dividir 18 entre 12, quédanos cociente 1 e resto tamén 6. No reloxo, isto significa que as 18 son as 6.

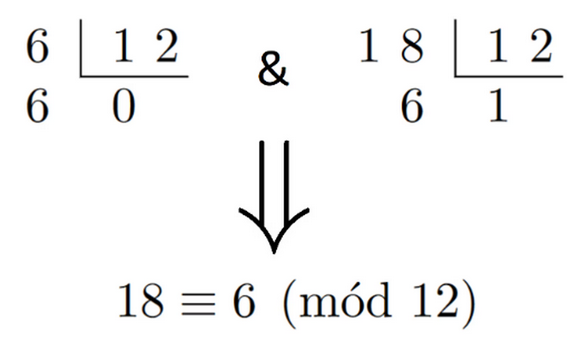
Esta é a notación matemática que se utiliza para expresar congruencias

Do mesmo xeito que na nosa numeración usual, na aritmética modular tamén podemos operar: se temos dous pares de números que son congruentes módulo n, tamén o serán as súas sumas; e o mesmo ocorre para résta e a multiplicación.

Para o DNI utilízase a congruencia módulo 23. O procedemento consiste en calcular o resto de dividir o número do DNI entre 23. En función deste resto, asígnaselle unha letra de acordo con a táboa que se mostra na imaxe inferior.

Así, se ao introducir o noso DNI cometemos algún pequeno erro, o novo número non se corresponderá coa letra introducida e saltará un aviso en calquera computador. A letra do DNI non é o único díxito de control que se calcula con congruencias: tamén o IBAN das contas bancarias.

FONTE: Alba García Ruíz e Javier Peñafiel/elpais.com/ciencia    Imaxe: gaussianos.com