A DISTANCIA MÁIS CURTA ENTRE DOUS PUNTOS NON É SEMPRE A LIÑA RECTA

Sabemos que a luz sempre toma o camiño máis curto entre dous puntos, que xeralmente consideramos unha liña recta. Con todo, unha liña recta é só a distancia máis curta entre dous puntos nunha superficie plana. Temos que remontarnos aos postulados de Euclides de Alexandría, considerado por moitos como o matemático máis importante da historia, quen afirmaba que a luz viaxaba en liña recta e demostraba que unha liña recta é máis curta que outras dúas liñas rectas que unen os mesmos extremos (sen ter en conta as curvas). Pero este teorema falla para xeometrías non euclidianas, como esferas e xeometrías máis complexas. De feito, todo o que aprendiches no colexio, como que as liñas paralelas mantéñense paralelas, só refírense á xeometría euclidiana. No universo non euclidiano, as liñas paralelas poden en realidade diverxer ou converxer.

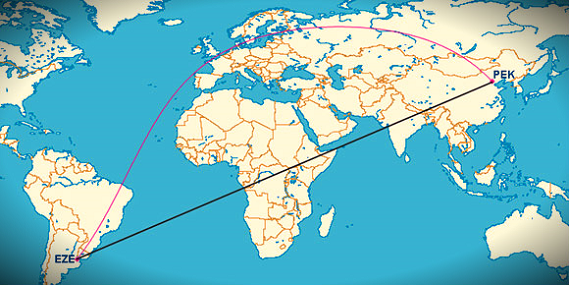
Pero lembremos que a Terra non é plana, senón que é aproximadamente unha esfera. Se vivísemos nunha Terra plana, se que poderiamos dicir que unha liña recta sería a distancia máis curta entre os puntos A e B. Pero xa dixemos que a Terra ten forma de esfera; para facelo mediante unha liña recta teriamos que atravesar a Terra e a distancia máis curta entre dous puntos nesta forma xeométrica é un arco coñecido como "a distancia do gran círculo". Así, nunha superficie curva, a distancia máis curta entre dous puntos é en realidade unha curva, tecnicamente coñecida como geodésica: son as traxectorias dadas polos “círculos máximos”. É o círculo máximo que os une.

É un concepto novo? De ningunha maneira. Para visualizalo mellor, pensemos no roteiro máis reducido dun avión que voa entre Londres e Nova York. O roteiro segue un camiño de "gran círculo" en lugar do que parece ser unha liña recta máis directa nun mapa plano. As roteiros curvas nestes destinos non se empregan aleatoriamente, senón que se utilizan porque en realidade representan a distancia máis curta entre dúas localizacións determinadas do noso planeta.

Se combinamos este concepto co principio de equivalencia de Einstein, na teoría da relatividade xeral, na que a gravidade pode dobrar a forma do espazo e o tempo, entón parecería que a luz en presenza de gravidade segue unha traxectoria curva ou, dito doutra maneira, a gravidade dobra o camiño da luz, como comentamos. Así, resulta que a gravidade non é máis que un espazo curvo ou, máis especificamente, a curvatura ou deformación do espazo-tempo de catro dimensións.

O camiño da Terra a medida que viaxa polo espazo inclínase constantemente cara ao Sol desta maneira, tanto que o planeta traza unha órbita case circular. Con todo, desde a perspectiva da cuarta dimensión, pódese ver que a Terra está simplemente seguindo o camiño máis curto ao longo dunha geodésica a través do espazo-tempo curvo.

Con todo o avanzado, incluso as grandes distancias circulares non representan a verdadeira distancia máis curta entre dúas localizacións dadas. Por que motivo? As distancias calcúlanse asumindo que a Terra é unha esfera perfecta, pero o planeta é máis unha esfera un pouco achatada con diferentes valores de radio cara ao ecuador e os polos. Por tanto, os valores do círculo máximo teñen unha tolerancia de aproximadamente ± 5%.

Un pouco de historia: os postulados de Euclides:

1.- Dados dous puntos pódense trazar unha recta que os une.

2.- Calquera segmento pode ser prolongado de forma continua nunha recta ilimitada na mesma dirección.

3.- É posible trazar unha circunferencia de centro en calquera punto e radio calquera.

4.- Todos os ángulos rectos son iguais.

5.- Se unha recta, ao cortar a outras dúas, forma os ángulos internos dun mesmo lado menores que dous rectos, ambas as rectas prolongadas indefinidamente córtanse ao lado no que están os ángulos menores que dous rectos. Ou o que é o mesmo: por un punto exterior a unha recta pódese trazar unha única paralela.

FONTE: Srah Romero/muyinteresante.es          Imaxe: azulweb.net