TEORÍA KAM

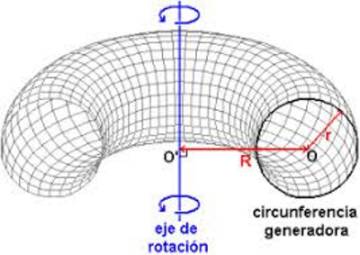
Este volume xeométrico ten forma dunha inofensiva rosquilla, e é o obxecto co que lida a teoría  KAM, un dos fitos matemáticos do pasado século  XX e a maior achega ao estudo dos sistemas dinámicos desde os traballos do matemático e físico  Henri  Poincaré en mecánica celeste a finais do  XIX. A teoría recibe o seu nome dos tres matemáticos que a descubriron:  Andréi  Kolmogorov,  Vladímir Arnold e  Jürgen  Moser ( KAM). Como nun festexo taurino, estes tres matemáticos loitaron contra os seus touros xeométricos.

Aínda que moitas persoas descoñézano, a palabra touro en castelán ten dúas acepcións: a primeira, do latín  tauros, refírese ao macho bovino adulto; símbolo do carácter poético e vital español para algúns, mártir nun bárbaro festexo para outros. A segunda acepción, proveniente do latín  torus, define a superficie de revolución procreada por unha circunferencia que rota ao redor dun eixo de  simetría contido no seu mesmo plano e exterior á circunferencia.

En 1954, durante o Congreso Internacional de Matemáticos celebrado en Ámsterdam,  Kolmogorov (Moscova, 1903-1987) saltou á area para expoñer unha nova e sorprendente teoría, que estudaba a estabilidade de certos sistemas dinámicos similares ao sistema solar. Cincuenta anos antes,  Poincaré sinalara que en sistemas de tres ou máis corpos celestes era moi complicado predicir con exactitude a traxectoria que seguiría cada un, debido ás interaccións  gravitacionales. Con todo,  Kolmogorov afirmou que, aínda que non podamos resolver explicitamente as ecuacións que rexen o sistema de maneira global, a maior parte da dinámica resiste pequenas perturbacións, e é, por tanto, predicible. Esta afirmación podería explicar a estabilidade das órbitas dos planetas, e que o sistema solar permaneza sempre tal e como o coñecemos. Nos anos posteriores, Arnold ( Odesa, 1937-2010), que tamén estudou en Moscova, e Moser ( Königsberg, 1928-1999), da escola alemá e posterior profesor do  MIT en EEUU, recibiron a alternativa de  Kolmogorov para proseguir co desenvolvemento da teoría  KAM.

A teoría  KAM estuda sistemas dinámicos próximos a  serintegrables. Dicimos que un sistema físico é  integrable se as ecuacións que o  modelizan poden resolverse. Pola contra, un sistema non é  integrable se non temos “suficientes pistas” para atopar fórmulas explícitas que determinen a súa evolución. En mecánica celeste, o modelo clásico de dous corpos orbitando un en torno ao outro, é un sistema  integrable, por exemplo, o sistema Terra-Sol vén descrito polas órbitas elípticas da terra fronte ao sol, e viceversa. Con todo, un terceiro corpo engadido ao modelo, como a Lúa, introduce perturbacións moi difíciles de predicir de maneira precisa en períodos longos de tempo (millóns de anos).

As ecuacións deste tipo de sistemas formúlanse no denominado espazo de fases, que está descrito polo conxunto de cada posición posible do sistema (configuración) e cada momento (unha variable física relacionada coa velocidade). Cando o sistema é  integrable, o espazo de fases está dividido en rexións con forma de touro, e estes son  invariantes baixo o réxime dinámico. Isto quere dicir que a órbita do sistema estará confinada nun dos touros xeométricos, sen abandonalo. Ademais, esta órbita é aproximadamente periódica, no sentido de que tras un intervalo de tempo, a órbita volve pasar preto da posición que ocupaba antes, pero non necesariamente a mesma. A estas traxectorias denomínaselles órbitas  cuasiperiódicas. Velaquí, pois, a cuestión fundamental da teoría  KAM: se se perturba un sistema  integrable lixeiramente (por exemplo, engadindo outro corpo relativamente pequeno), algúns destes touros se  deformarán xunto coas súas órbitas  cuasiperiódicas, pero sobrevivirán á perturbación, mentres que outros serán destruídos dando lugar a dinámicas caóticas.

No caso do noso Sistema Solar, é moi difícil saber se a órbita terrestre está confinada dentro dun touro  invariante ou pola contra segue un curso caótico. Os cálculos numéricos baseados na física clásica de Newton non descartan comportamentos caóticos da Terra para intervalos de poucos centos de millóns de anos. Con todo, simulacións numéricas realizadas a partir da Relatividade Xeral auguran unha maior estabilidade. Todo apunta a que durante os cinco mil millóns de anos de vida que, aproximadamente, quedan ao Sol, o sistema solar permanecerá relativamente tranquilo. En termos celestes, parece que habitamos a pel dun touro.

FONTE: Cristina Sardón Muñoz e Víctor Arnaiz Solórzano/elpais.es/ciencia